Primitive Set Operations in Eclipse Collections — Part 2

Primitive Set Operations in Eclipse Collections - Part 2

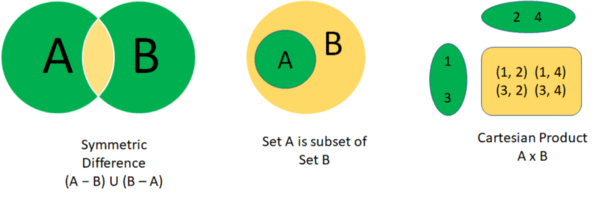
Continuing from Part 1, in the Eclipse Collections 11.0 release, we will have the following Set operations union, intersect, difference, symmetricDifference, isSubsetOf, isProperSubsetOf, cartesianProduct on primitive collections.

Set Operations that will be available on primitive sets in Eclipse Collections 11.0.

 

These APIs are already available on Sets on the object side, but my goal was to implement these methods for Sets supporting primitive types namely IntSet, LongSet, ShortSet, DoubleSet, FloatSet, CharSet, BooleanSet, ByteSet. Additionally, the above operations will be available in both mutable and immutable interfaces.

I covered the first three operations (union, intersect and difference) in this blog. I will talk about the remaining operations here.

Symmetric Difference — What does this operation do?

Method signature: setA.symmetricDifference(setB)

This operation returns a set that contains elements that are in either one of the two sets but not both. In other words, (Set A — Set B) U (Set B — Set A).

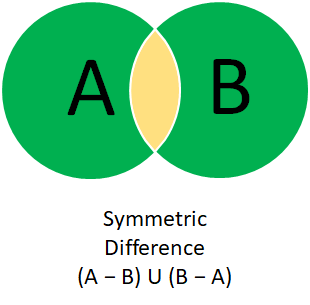
Set B — 2, 3, 4.

A — B = 1.

B — A= 4.

Symmetric Difference — 1, 4.

 Symmetric Difference — Code Implementation

🛈 Eclipse Collections has an existing API that allows us to reject that returns all the elements that evaluate false for the givenPredicate and results are added to a target collection. Predicate here is this::contains and target collection is the set returned from this.difference(set).

At this point of implementing symmetricDifference, we already had an API that can compute difference of Set A and Set B.

default MutableIntSet symmetricDifference(IntSet set)
{
    return set.reject(this::contains, this.difference(set));
}

Symmetric Difference — Usage

@Test
public void symmetricDifference()
{
    MutableIntSet setA = IntSets.mutable.with(1, 2, 3);
    MutableIntSet setB = IntSets.mutable.with(2, 3, 4);
    MutableIntSet expected = IntSets.mutable.with(1, 4);
    MutableIntSet actual = setA.symmetricDifference(setB);
    Assert.assertEquals(expected, actual);
}

Test cases covering various scenarios can be found here.

Is Subset of — What does this operation do?

Method signature: setA.isSubsetOf(setB)

This operation returns true if all elements from Set A are present in Set B.

 

Set B — 1, 2, 3.

Is Set A a subset of Set B — true.

Is Subset Of — Code Implementation

🛈 Eclipse Collections has an existing API called containsAll that evaluates to true if all the values in this are present in set.

default boolean isSubsetOf(IntSet set)
{
    return this.size() <= set.size() && set.containsAll(this);
}

Is Subset of — Usage

@Test
public void isSubsetOf()
{
    MutableIntSet setA = IntSets.mutable.with(1, 2);
    MutableIntSet setB = IntSets.mutable.with(1, 2, 3);
    Assert.assertTrue(setA.isSubsetOf(setB));

    MutableIntSet setC = IntSets.mutable.with(1, 2, 3);
    MutableIntSet setD = IntSets.mutable.with(1, 2, 3);
    Assert.assertTrue(setC.isSubsetOf(setD));
}

Test cases covering various scenarios can be found here.

Is Proper Subset of — What does this operation do?

Method signature: setA.isProperSubsetOf(setB)

This operation returns true if all elements of Set A are present in Set B but the two sets are not equal i.e. there is at least one element in Set B that is not present in Set A.

Is Proper Subset of —Code Implementation

default boolean isProperSubsetOf(IntSet set)
{
    return this.size() < set.size() && set.containsAll(this);
}

Is Proper Subset of — Usage

@Test
public void isProperSubsetOf()
{
    MutableIntSet setA = IntSets.mutable.with(1, 2);
    MutableIntSet setB = IntSets.mutable.with(1, 2, 3);
    Assert.assertTrue(setA.isProperSubsetOf(setB));

    MutableIntSet setC = IntSets.mutable.with(1, 2, 3);
    MutableIntSet setD = IntSets.mutable.with(1, 2, 3);
    Assert.assertFalse(setC.isProperSubsetOf(setD));
}

Test cases covering various scenarios can be found here.

Cartesian Product — What does this operation do?

Method Signature: setA.cartesianProduct(setB)

Cartesian Product of Set A and Set B is the set of all possible ordered pairs where the first element of the pair is from Set A and the second element from Set B.

 

Set A — 1, 3.

Set B — 2, 4.

Cartesian Product —

{(1, 2), (1, 4), (3, 2). (3, 4)}.

Cartesian Product — Code Implementation

🛈 Eclipse Collections has a static utility class called IntSets and equivalent classes for other primitive set collections.

@Override
public LazyIterable<IntIntPair> cartesianProduct(IntSet set)
{
    return IntSets.cartesianProduct(this, set);
}

Below code is the underlying cartesianProduct implementation.

public static <A, B, C> LazyIterable<C> cartesianProduct(IntSet set1, IntSet set2, IntIntToObjectFunction<C> function)
{
    return set1.asLazy()
            .flatCollect(first ->
                set2.asLazy()
                    .collect(second -> function.value(first, second)));
}

Cartesian Product — Usage

@Test
public void cartesianProduct()
{
    MutableIntSet setA = IntSets.mutable.with(1, 3);
    MutableIntSet setB = IntSets.mutable.with(2, 4);
    MutableSet<IntIntPair> expected = Sets.mutable.with(
            PrimitiveTuples.pair(1, 2),
            PrimitiveTuples.pair(1, 4),
            PrimitiveTuples.pair(3, 2),
            PrimitiveTuples.pair(3, 4));
    Assert.assertEquals(expected, 
            setA.cartesianProduct(setB).toSet());
}

Test cases covering various scenarios can be found here.

I am a committer for the Eclipse Collections OSS project at Eclipse Foundation. Eclipse Collections is open for contributions and if you like our library, let us know by starring our GitHub repository.