Rolling Binary Trees: A Guide to Common Design Patterns in Java

Introduction

Binary trees are fundamental data structures, ubiquitous in computer science and software engineering. We use them to represent hierarchical data and implement more complex data structures, such as search trees, syntax trees, cryptographic hash trees, space partitioning trees, heaps, and so on. Common binary tree operations include insertion, deletion, traversal, and rotation.

A relatively uncommon and unexplored operation is roll, which modifies the structure of a binary tree in such a way that, when visualized, the newly obtained structure appears to be rolled at a 90-degree angle, either clockwise or counterclockwise. This gives us two variants of the roll operation — clockwise roll (CR) and counterclockwise roll (CCR).

Unlike rotation, which renders the inorder traversal of a binary tree invariant, rolling a binary tree produces a new binary tree whose inorder traversal is identical to (a) the postorder traversal of the original tree, if rolled clockwise; or (b) the preorder traversal of the original tree, if rolled counterclockwise. Inversely, the inorder traversal of the original tree becomes (a) the preorder traversal of the clockwise-rolled tree, or (b) the postorder traversal of the counterclockwise-rolled tree. Formally, we can define the roll operation in terms of these traversals, as follows:

• CR(T1) = (T2) ↔ Postorder(T1) = Inorder(T2) & Inorder(T1) = Preorder(T2)
• CCR(T1) = (T2) ↔ Preorder(T1) = Inorder(T2) & Inorder(T1) = Postorder(T2)

where T1 is the original tree, T2 is the rolled tree, and ↔ denotes equivalence.

We can deduce that the two roll variants are inverse to one another, i.e., applying the roll operation to a binary tree twice in succession in opposite directions always produces the original tree.

Binary tree roll examples

Below is a simple illustration of a binary tree (T1) and its clockwise-rolled counterpart (T2) to its right. Due to the inverse nature of the roll variants, we can also say that T1 is the counterclockwise-rolled counterpart of T2.

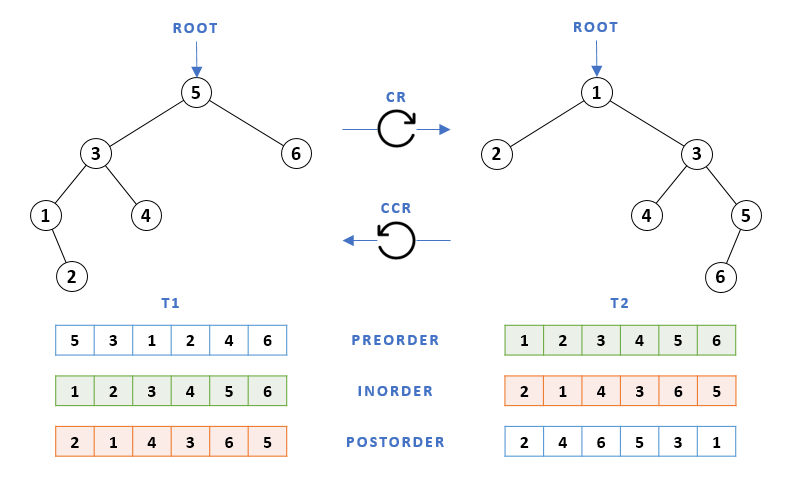
In some cases, when the topology of the tree is such that when viewed at a ±90° angle it appears as though certain nodes have two parents, the visual effect of the roll transformation may lose its acuity. Nevertheless, the equivalence between the correlated traversals always holds. For instance, consider the binary tree T2 from the previous example and its clockwise-rolled counterpart T3 shown below.

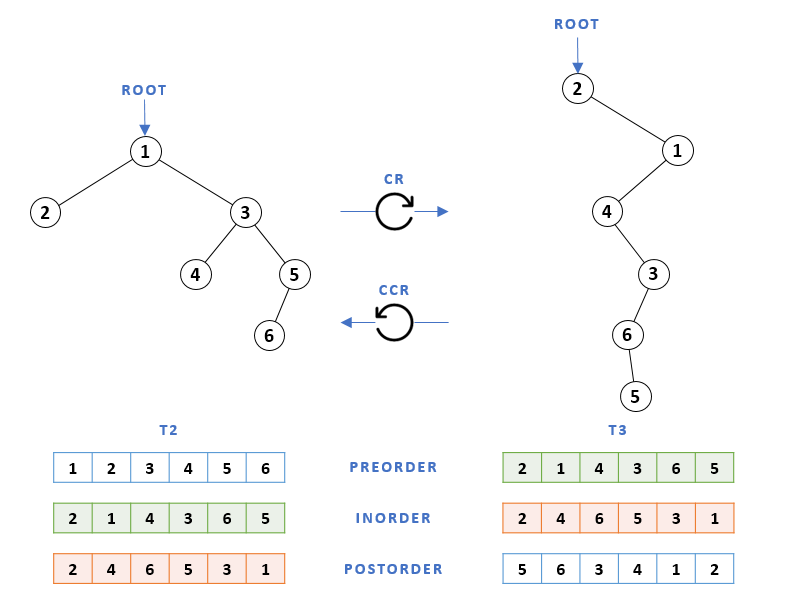
If we compare T3 to a literal -90° view of T2, the subtrees rooted at nodes ④ and ⑥ appear to be "pulled down" to create a proper binary tree structure. A similar thing happens when we take T3 from the example above and roll it clockwise.

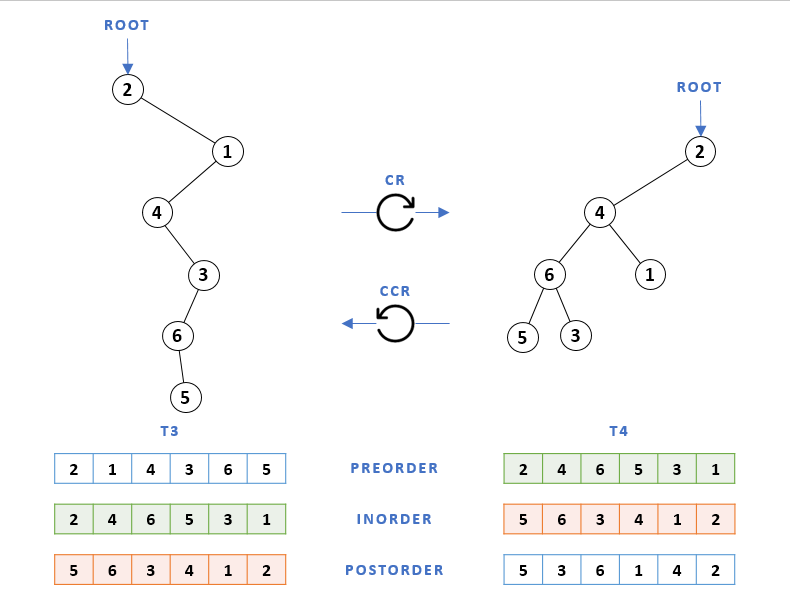
This time we get a rolled tree that has the same root as the original tree, since T3's root node is also its leftmost node. And the subtrees rooted at ④ and ⑥ appear to be adjusted again, to correct for the aforementioned double-parent "anomaly."

Pseudocode and complexity

def cRoll(root, parent = null) 
    if root != null
        if root.left != null
            cRoll(root.left, parent)
            root.left.right = root
            root.left = null
        else if parent != null
            parent.left = root
            parent.right = null
        if root.right != null
            cRoll(root.right, root)

We model the roll operation as a recursive algorithm that takes a binary tree (i.e., a reference to its root node) as input and mutates its topology in place. The algorithm traverses the tree in a depth-first manner, removing existing and creating new links between the nodes as it goes. As a result, it produces a modified version of the original tree in accordance with the definition of the roll operation. A special parameter parent is used to anchor subtrees constructed during the recursive traversal to their target parent nodes.

The algorithm has a time complexity of Θ(𝑛), where 𝑛 is the number of nodes in the tree, and its space complexity is proportional to the height of the binary tree (ℎ) as the call stack grows up to ℎ + 1 frames, i.e., Θ(𝑛) in the worst case (for ℎ = 𝑛 - 1) and Θ(log₂ 𝑛) in the best case (for ℎ = ⌊log₂ 𝑛⌋).

For a detailed analysis of this algorithm and its complexity, please refer to the following paper: A linear time algorithm for rolling binary trees.

Implementation

In this section, we are going to present a step by step implementation of the binary tree roll algorithm in Java, by following basic design principles of object-oriented programming and implementing a few design patterns along the way.

Project setup

Let's start by bootstrapping a new Java project using Maven. We are going to use the JUnit 5 framework to test our implementation, so we need to add the following dependency to the pom.xml file of the project:

<dependencies>
  <dependency>
    <groupId>org.junit.jupiter</groupId>
    <artifactId>junit-jupiter</artifactId>
    <version>5.9.2</version>
    <scope>test</scope>
  </dependency>
</dependencies>

Now let's define the basic building blocks of our implementation, i.e., the binary tree data structure and the tree traversal algorithms. We begin by creating a simple, recursively defined Node class that holds a value of a generic type T and references to its left and right children.

public class Node<T> {
    private T value;
    private Node<T> left
    private Node<T> right;

    /* constructors, getters, setters, etc. */
}

Static factory methods

With the recursive Node structure in place, we create a BinaryTree class that holds a reference to the root node of the tree and provides a static factory method for creating new instances of the class from a list of values provided in a nullable level-order traversal format. This format uses a "null identifier" value to denote empty (null) nodes. For example, the sequence [1, 2, 3, -1, -1, 4, 5, -1, 6],  where -1 is the null identifier, represents the following binary tree:

  1
 / \
2   3
   / \
  4   5
   \  
    6

The way we can implement the static factory method is by using a queue to store the nodes of the tree as we parse them from the input sequence. First, we add the root node to the queue. Then, we read the next two values from the input sequence and create the left and right children of the node. If a node value is null, we do not create a child node. We add the newly created children to the queue and repeat this process until we reach the end of the input sequence.

public class BinaryTree<T> {
  
  private Node<T> root;

  private BinaryTree(Node<T> root) {
    this.root = root;
  }

  public static <T> BinaryTree<T> of(T[] values, T nullIdentifier) {
    if (values == null || values.length == 0 || values[0] == nullIdentifier) {
      return new BinaryTree<>();
    }

    Node<T> rootNode = new Node<>(values[0]);
    Queue<Node<T>> nodeQueue = new LinkedList<>();
    nodeQueue.offer(rootNode);

    int valPtr = 1;

    while (!nodeQueue.isEmpty()) {
      T leftVal = (valPtr < values.length) ? values[valPtr++] : null;
      T rightVal = (valPtr < values.length) ? values[valPtr++] : null;
      Node<T> node = nodeQueue.poll();

      if (leftVal != null && !leftVal.equals(nullIdentifier)) {
        Node<T> leftNode = new Node<>(leftVal);
        node.setLeft(leftNode);
        nodeQueue.offer(leftNode);
      }

      if (rightVal != null && !rightVal.equals(nullIdentifier)) {
        Node<T> rightNode = new Node<>(rightVal);
        node.setRight(rightNode);
        nodeQueue.offer(rightNode);
      }
    }

    return new BinaryTree<>(rootNode);
  }
}

For convenience, we also create an overloaded version of the static factory method of that uses null as the default null identifier value, and a single, varargs input parameter:

public static <T> BinaryTree<T> of(T... values) {
  return of(values, null);
}

The Visitor pattern

To obtain the preorder, inorder, and postorder traversals of the binary tree, we can make use of the Visitor design pattern. This will allow us to separate the traversal algorithms from the binary tree data structure and avoid unnecessary coupling.

First, we define an interface for the visitor that we will use to traverse the nodes of the tree:

public interface Visitor<T> {
  void visit(Node<T> node);
}

Then, we create three concrete implementations of the Visitor interface, one for each of the three traversal orders. We want these visitors to store the nodes in a list in the order in which they are visited. And since the action we want to perform on the nodes (i.e., adding them to a list) is the same for all traversals, we implement it with a separate interface, called VisitorAction, and pass it to the visitors as a constructor argument. This design decouples the traversal logic from the action we perform on the visited nodes, which makes the code even cleaner and more flexible.

The implementation of the VisitorAction interface and one of the concrete visitors is shown below. We extend Java's Consumer functional interface to allow custom actions and composed (chained) consumers to be passed at runtime.

public interface VisitorAction<T> extends Consumer<Node<T>> {
  
  @Override
  default VisitorAction<T> andThen(Consumer<? super Node<T>> after) {
    return Consumer.super.andThen(after)::accept;
  }
}

public final class PreorderVisitor<T> implements Visitor<T> {
  private final VisitorAction<T> action;

  public PreorderVisitor(VisitorAction<T> action) {
    this.action = action;
  }

  public VisitorAction<T> action() {
    return action;
  }

  @Override
  public void visit(Node<T> root) {
    if (root != null) {
      action.accept(root);
      this.visit(root.getLeft());
      this.visit(root.getRight());
    }
  }
}

We can now define the concrete action for adding the visited nodes to a list:

public class NodeCollectorVisitorAction<T> implements VisitorAction<T> {

  private final List<T> list;

  public NodeCollectorVisitorAction() {
    this.list = new ArrayList<>();
  }

  public List<T> getList() {
    return list;
  }

  @Override
  public void accept(Node<T> node) {
    list.add(node.getValue());
  }
}

To complete our traversal functionality, we introduce another level of abstraction and make the Node and the BinaryTree classes traversable by our visitors through a generic interface, as follows:

public interface Traversable<T> {
  void traverse(Visitor<T> visitor);
}

public class Node<T> implements Traversable<T> {
  /* ... */

  @Override
  public void traverse(Visitor<T> visitor) {
    visitor.visit(this);
  }
}

public class BinaryTree<T> implements Traversable<T> {
  /* ... */
  
  @Override
  public void traverse(Visitor<T> visitor) {
    if (this.root == null) throw new IllegalStateException("Cannot traverse an empty tree");
    this.root.traverse(visitor);
  }
}

Before we move on to the implementation of the roll operation, let's create a simple test for the BinaryTree class to make sure that the tree is created correctly from the input sequence:

@Test
void testTraversals() {
  Integer[] values = {1, 2, 3, null, null, 4, 5, null, 6};
  BinaryTree<Integer> tree = BinaryTree.of(values);

  var preorderCollector = new NodeCollectorVisitorAction<Integer>();
  var inorderCollector = new NodeCollectorVisitorAction<Integer>();
  var postorderCollector = new NodeCollectorVisitorAction<Integer>();

  tree.traverse(new PreorderVisitor<>(preorderCollector));
  tree.traverse(new InorderVisitor<>(inorderCollector));
  tree.traverse(new PostorderVisitor<>(postorderCollector));

  var expectedPreorder = List.of(1, 2, 3, 4, 6, 5);
  var expectedInorder = List.of(2, 1, 4, 6, 3, 5);
  var expectedPostorder = List.of(2, 6, 4, 5, 3, 1);

  assertEquals(expectedPreorder, preorderCollector.getList());
  assertEquals(expectedInorder, inorderCollector.getList());
  assertEquals(expectedPostorder, postorderCollector.getList());
}

Let's also show the flexibility of our visitors by refactoring our test with lambda expressions:

@Test
void testTraversalsWithLambdas() {
  var tree = BinaryTree.of(1, 2, 3, null, null, 4, 5, null, 6);

  var preorderList = new ArrayList<Integer>();
  var inorderList = new ArrayList<Integer>();
  var postorderList = new ArrayList<Integer>();

  tree.traverse(new PreorderVisitor<>(node -> preorderList.add(node.getValue())));
  tree.traverse(new InorderVisitor<>(node -> inorderList.add(node.getValue())));
  tree.traverse(new PostorderVisitor<>(node -> postorderList.add(node.getValue())));

  assertEquals(List.of(1, 2, 3, 4, 6, 5), preorderList);
  assertEquals(List.of(2, 1, 4, 6, 3, 5), inorderList);
  assertEquals(List.of(2, 6, 4, 5, 3, 1), postorderList);
}

The binary tree roll algorithm

To implement the algorithm for rolling binary trees, we need to consider the two roll directions, clockwise and counterclockwise. We also need to take into account the fact that, in most cases, the root node of the rolled tree is not going to be the same as the root node of the original tree.

This means that we need to implement a mechanism to identify and store a reference to the root node of the rolled tree. A good way to do this would be by creating an abstract class called RollHandler, which we can use as a base class for the concrete implementations of the algorithm.

abstract class RollHandler<T> {

  private Node<T> rolledRoot;

  public Node<T> getRolledRoot() {
    return rolledRoot;
  }

  public void setRolledRoot(Node<T> rolledRoot) {
    this.rolledRoot = rolledRoot;
  }

  abstract void roll(Node<T> root, Node<T> parent);
}

We will implement the roll method for the clockwise and the counterclockwise roll variants separately, and have these implementations use the rolledRoot field to assign a reference to the rolled tree's root node.

We can identify the rolled tree's root node when the recursive traversal reaches either the leftmost or the rightmost node of the original tree, depending on the roll direction. This means that we can obtain a reference to it in the else block of the algorithm, when we have reached a node without a left child (when performing the clockwise roll) or without a right child (when performing the counterclockwise roll), and when the parent argument is also null. The latter condition ensures that we have reached the leftmost (or the rightmost) node of the original tree, rather than one of its subtrees.

The implementation of the roll method for the clockwise and counterclockwise roll handlers will, therefore, look something like this:

class ClockwiseRollHandler<T> extends RollHandler<T> {

  @Override
  public void roll(Node<T> root, Node<T> parent) {
    if (root != null) {
      if (root.getLeft() != null) {
        this.roll(root.getLeft(), parent);
        root.getLeft().setRight(root);
        root.setLeft(null);
      } else {
        if (parent != null) {
          parent.setLeft(root);
          parent.setRight(null);
        } else {
          this.setRolledRoot(root);
        }
      }

      if (root.getRight() != null) {
        this.roll(root.getRight(), root);
      }
    }
  }
}

class CounterclockwiseRollHandler<T> extends RollHandler<T> {

  @Override
  public void roll(Node<T> root, Node<T> parent) {
    if (root != null) {
      if (root.getRight() != null) {
        this.roll(root.getRight(), parent);
        root.getRight().setLeft(root);
        root.setRight(null);
      } else {
        if (parent != null) {
          parent.setRight(root);
          parent.setLeft(null);
        } else {
          this.setRolledRoot(root);
        }
      }

      if (root.getLeft() != null) {
        this.roll(root.getLeft(), root);
      }
    }
  }
}

To mutate or not to mutate?

Aside from the two different roll variants, there is another important implementation aspect we need to consider. And that is the fact that mutating the original data structure might not always be desirable.

There might be use cases where we want to preserve the original tree, and for this reason, we will provide two different top-level implementations of the roll algorithm: one that mutates the original tree, and one that preserves the original tree and creates a new one.

A Factory of Strategies

We can combine the Strategy and the Factory design patterns to create the mutating (mutable) and non-mutating (immutable) versions of the clockwise and counterclockwise roll algorithm, and to allow the user to choose the desired implementation at runtime.

First, we define an interface for the roll strategy:

public interface RollStrategy<T> {
  BinaryTree<T> roll(BinaryTree<T> tree);
}

Then, we create two abstract classes that implement the RollStrategy interface and provide two different templates for implementing the roll algorithm. This approach is also known as the Template Method pattern, where an abstract superclass defines the high-level skeleton of an algorithm.

Both templates will have an abstract method to obtain a roll handler. And for the immutable strategy, we will apply the roll method of the roll handler to a deep copy of the tree, keeping the original tree intact:

abstract class DefaultRollStrategy<T> implements RollStrategy<T> {

  @Override
  public BinaryTree<T> roll(BinaryTree<T> tree){
    var rollHandler = getRollHandler();
    rollHandler.setRolledRoot(null);
    rollHandler.roll(tree.getRoot(), null);
    tree.setRoot(rollHandler.getRolledRoot());
    return tree;
  }

  abstract RollHandler<T> getRollHandler();
}

abstract class ImmutableRollStrategy<T> implements RollStrategy<T> {

  @Override
  public BinaryTree<T> roll(BinaryTree<T> tree) {
    var rollHandler = getRollHandler();
    rollHandler.setRolledRoot(null);
    var treeCopy = tree.deepCopy();
    rollHandler.roll(treeCopy.getRoot(), null);
    treeCopy.setRoot(rollHandler.getRolledRoot());
    return treeCopy;
  }

  abstract RollHandler<T> getRollHandler();
}

The deepCopy method runs recursively on the root node and creates a deep clone of the tree.

public BinaryTree<T> deepCopy() {
  return new BinaryTree<>(root != null ? root.deepCopy() : null);
}

public Node<T> deepCopy() {
  var copy = new Node<>(this.value);

  if (this.left != null) {
    copy.setLeft(this.left.copy());
  }

  if (this.right != null) {
    copy.setRight(this.right.copy());
  }

  return copy;
}

To combine the mutable and immutable strategy templates with the clockwise and counterclockwise roll handlers, we create concrete roll strategies which extend the abstract RollStrategy classes and implement the getRollHandler method. For simplicity, we nest the immutable roll strategies inside the default (mutable) roll strategy classes:

final class ClockwiseRollStrategy<T> extends DefaultRollStrategy<T> {

  @Override
  RollHandler<T> getRollHandler() {
    return new ClockwiseRollHandler<>();
  }

  static final class Immutable<T> extends ImmutableRollStrategy<T> {

    @Override
    RollHandler<T> getRollHandler() {
      return new ClockwiseRollHandler<>();
    }
  }
}

final class CounterclockwiseRollStrategy<T> extends DefaultRollStrategy<T> {

  @Override
  RollHandler<T> getRollHandler() {
    return new CounterclockwiseRollHandler<>();
  }

  static final class Immutable<T> extends ImmutableRollStrategy<T> {

    @Override
    RollHandler<T> getRollHandler() {
      return new CounterclockwiseRollHandler<>();
    }
  }
}

Next, we create a factory interface that we can use to obtain instances of the roll strategies. We use switch expressions to return a strategy in a concise and elegant way.

public enum RollDirection {
  CLOCKWISE,
  COUNTER_CLOCKWISE
}

public interface RollStrategyFactory {

  static <T> RollStrategy<T> create(RollDirection direction) {
    return switch (direction) {
      case CLOCKWISE -> new ClockwiseRollStrategy<>();
      case COUNTER_CLOCKWISE -> new CounterClockwiseRollStrategy<>();
    };
  }

  static <T> RollStrategy<T> createImmutable(RollDirection direction) {
    return switch (direction) {
      case CLOCKWISE -> new ClockwiseRollStrategy.Immutable<>();
      case COUNTER_CLOCKWISE -> new CounterClockwiseRollStrategy.Immutable<>();
    };
  }
}

Finally, we add a roll method to the BinaryTree class that accepts a RollStrategy instance as an argument and invokes its roll method on the tree:

public class BinaryTree<T> {
  /* ... */
  
  public BinaryTree<T> roll(RollStrategy<T> strategy) {
    return strategy.roll(this);
  }
}

Note that the BinaryTree class does not have to be aware of the roll strategies, so if we want to keep the code as loosely coupled as possible, we can skip this step, and let the user invoke the RollStrategy.roll method directly and pass the tree they want to roll as an argument.

Design for extension, or else prohibit it

Rolling a binary tree is a straightforward operation with a finite number of variants, and we have implemented both mutable and immutable versions of these variants, exhausting all possible use case scenarios. To create a closed hierarchy of roll strategies and prevent side effects that could break the algorithm, we can seal the RollStrategy interface and all abstract classes below it by declaring them sealed and associating them with their intended inheritors or implementers.

public sealed interface RollStrategy<T> 
    permits ClockwiseRollStrategy, CounterclockwiseRollStrategy {
  /* ... */
}

abstract sealed class DefaultRollStrategy<T> implements RollStrategy<T> 
    permits ClockwiseRollStrategy, CounterclockwiseRollStrategy {
  /* ... */
}

abstract sealed class ImmutableRollStrategy<T> implements RollStrategy<T> 
    permits ClockwiseRollStrategy.Immutable, CounterClockwiseRollStrategy.Immutable {
  /* ... */
}

abstract sealed class RollHandler<T> 
    permits ClockwiseRollHandler, CounterClockwiseRollHandler {
  /* ... */
}

Testing

We can now use our roll algorithm implementation to roll binary trees clockwise and counterclockwise. But before we do that, let's create a simple helper class that we can use to print binary trees to the console. We will use a basic recursive algorithm that prints the tree in a sideways, left-to-right fashion.

public class BinaryTreePrinter<T> {

  private final PrintStream printStream;
  private final int edgeLength = 4;
  private final String edgeShapes = " ┘┐┤";

  public BinaryTreePrinter(PrintStream printStream) {
    this.printStream = printStream;
  }

  public void printTree(BinaryTree<T> tree) {
    var root = tree.getRoot();

    if (root == null) {
      printStream.println("NULL");
    }

    printStream.println(printTree(root, 1, ""));
  }

  private String printTree(BinaryTree.Node<T> root, int direction, String prefix) {
    if (root == null) {
      return "";
    }

    var edgeType = (root.getRight() != null ? 1 : 0) + (root.getLeft() != null ? 2 : 0);

    var postfix = switch (edgeType) {
      case 1, 2, 3 -> " " + "—".repeat(edgeLength) + edgeShapes.charAt(edgeType) + "\n";
      default -> "\n";
    };

    var padding = " ".repeat(edgeLength + root.getValue().toString().length());

    var printRight = print(root.getRight(), 2, prefix + "│  ".charAt(direction) + padding);
    var printLeft = print(root.getLeft(), 0, prefix + "  │".charAt(direction) + padding);

    return printRight + prefix + root.getValue() + postfix + printLeft;
  }
}

Next, let's set up a test class that we can use to test our complete implementation.

class IntegrationTests<T> {

  private NodeCollectorVisitorAction<T> preorderCollector1, inorderCollector1, postorderCollector1;
  private NodeCollectorVisitorAction<T> preorderCollector2, inorderCollector2, postorderCollector2;

  private final BinaryTreePrinter<T> printer = new BinaryTreePrinter<>(System.out);

  @BeforeEach
  void setUp() {
    preorderCollector1 = new NodeCollectorVisitorAction<>();
    preorderCollector2 = new NodeCollectorVisitorAction<>();
    inorderCollector1 = new NodeCollectorVisitorAction<>();
    inorderCollector2 = new NodeCollectorVisitorAction<>();
    postorderCollector1 = new NodeCollectorVisitorAction<>();
    postorderCollector2 = new NodeCollectorVisitorAction<>();
  }
}

Now, let's create a small binary tree, roll it clockwise, and print the results to the console.

void testClockwiseRoll() {
  var tree = BinaryTree.of("Friends", "Jay", "Open", "Foo", "IO", "Of", "JDK");
  printer.printTree(tree);

  tree.traverse(new PreorderVisitor<String>(preorderCollector1));
  tree.traverse(new InorderVisitor<String>(inorderCollector1));
  tree.traverse(new PostorderVisitor<String>(postorderCollector1));

  System.out.println(preorderCollector1.getList());
  System.out.println(inorderCollector1.getList());
  System.out.println(postorderCollector1.getList());
  System.out.println();

  tree.roll(RollStrategyFactory.create(RollDirection.CLOCKWISE));
  printer.printTree(tree);

  tree.traverse(new PreorderVisitor<String>(preorderCollector2));
  tree.traverse(new InorderVisitor<String>(inorderCollector2));
  tree.traverse(new PostorderVisitor<String>(postorderCollector2));

  System.out.println(preorderCollector2.getList());
  System.out.println(inorderCollector2.getList());
  System.out.println(postorderCollector2.getList());
  System.out.println();
  
  assertEquals(postorderCollector1.getList(), inorderCollector2.getList());
  assertEquals(inorderCollector1.getList(), preorderCollector2.getList());
}

                     JDK
            Open ————┤
            │        Of
Friends ————┤
            │       IO
            Jay ————┤
                    Foo

[Friends, Jay, Foo, IO, Open, Of, JDK]
[Foo, Jay, IO, Friends, Of, Open, JDK]
[Foo, IO, Jay, Of, JDK, Open, Friends]

                Friends ————┐
                │           │      Open ————┐
                │           │      │        JDK
                │           Of ————┘
        Jay ————┤
        │       IO
Foo ————┘

[Foo, Jay, IO, Friends, Of, Open, JDK]
[Foo, IO, Jay, Of, JDK, Open, Friends]
[IO, JDK, Open, Of, Friends, Jay, Foo]

Let's also test the immutable strategy, this time with the counterclockwise roll variant:

void testImmutableCounterClockwiseRoll() {
  var tree = BinaryTree.of("Friends", "Jay", "Open", "Foo", "IO", "Of", "JDK");
  printer.printTree(tree);

  tree.traverse(new PreorderVisitor<>(preorderCollector1));
  tree.traverse(new InorderVisitor<>(inorderCollector1));
  tree.traverse(new PostorderVisitor<>(postorderCollector1));

  System.out.println(preorderCollector1.getList());
  System.out.println(inorderCollector1.getList());
  System.out.println(postorderCollector1.getList());
  System.out.println();

  var rolledTree = tree.roll(RollStrategyFactory.createImmutable(RollDirection.COUNTER_CLOCKWISE));
  printer.printTree(rolledTree);

  rolledTree.traverse(new PreorderVisitor<>(preorderCollector2));
  rolledTree.traverse(new InorderVisitor<>(inorderCollector2));
  rolledTree.traverse(new PostorderVisitor<>(postorderCollector2));

  System.out.println(preorderCollector2.getList());
  System.out.println(inorderCollector2.getList());
  System.out.println(postorderCollector2.getList());
  System.out.println();

  printer.printTree(tree);
  
  assertEquals(preorderCollector1.getList(), inorderCollector2.getList());
  assertEquals(inorderCollector1.getList(), postorderCollector2.getList());
}

                     JDK
            Open ————┤
            │        Of
Friends ————┤
            │       IO
            Jay ————┤
                    Foo

[Friends, Jay, Foo, IO, Open, Of, JDK]
[Foo, Jay, IO, Friends, Of, Open, JDK]
[Foo, IO, Jay, Of, JDK, Open, Friends]

JDK ————┐
        │        Of
        Open ————┤
                 │           IO ————┐
                 │           │      │       Foo
                 │           │      Jay ————┘
                 Friends ————┘

[JDK, Open, Friends, IO, Jay, Foo, Of]
[Friends, Jay, Foo, IO, Open, Of, JDK]
[Foo, Jay, IO, Friends, Of, Open, JDK]

                     JDK
            Open ————┤
            │        Of
Friends ————┤
            │       IO
            Jay ————┤
                    Foo

As we can see, the immutable strategy constructed the rolled tree properly, while preserving the state of the original tree.

Summary

In this article, we introduced a linear time algorithm for rolling binary trees and implemented it in Java. We relied on common design patterns and principles to make the implementation clean and flexible, while ensuring appropriate encapsulation and loose coupling between the components.

First, we showed how we can use generics and static factory methods to create data structures, such as binary trees, with a convenient syntax similar to the one used in the Java Collections & Map APIs. Then, we made use of the Visitor pattern to implement the preorder, inorder, and postorder tree traversals. We used the Strategy pattern to implement the clockwise and counterclockwise variants of the binary tree roll algorithm, and we utilized the Template Method pattern to create mutable and immutable versions of each variant. Finally, we used the Factory pattern to expose the roll strategies and made the underlying types sealed to prevent the creation of custom strategies.

To wrap things up, we implemented a helper class to visualize the results of the roll algorithm and used it along with the tree traversing visitors to test the correctness of our implementation.

The complete source code referenced in this article can be found here.

• Java Core
• Maven
• Research
• Sealed Classes
• Tutorials
• Use Cases

George Tanev

Author

Multifaceted software engineer with a computer science background and research published by IEEE, OEIS, and Springer. Experienced in designing, developing, and deploying web and desktop applications, data pipelines, and custom software solutions. Worked with organizations across a range of industries and consulted for clients such as MIT, Triplebyte, and Rollbar.